Thalamocortical circuit
Information from the sensory surround transmits through the nuclei of the thalamus en route to the cortex. The thalmic reticular nucleus (TRN) sits between these structures and shapes thalamic activity through the inhibitory synapses sent to thalamus. TRN cells notably communicate with each other using electrical synapses.
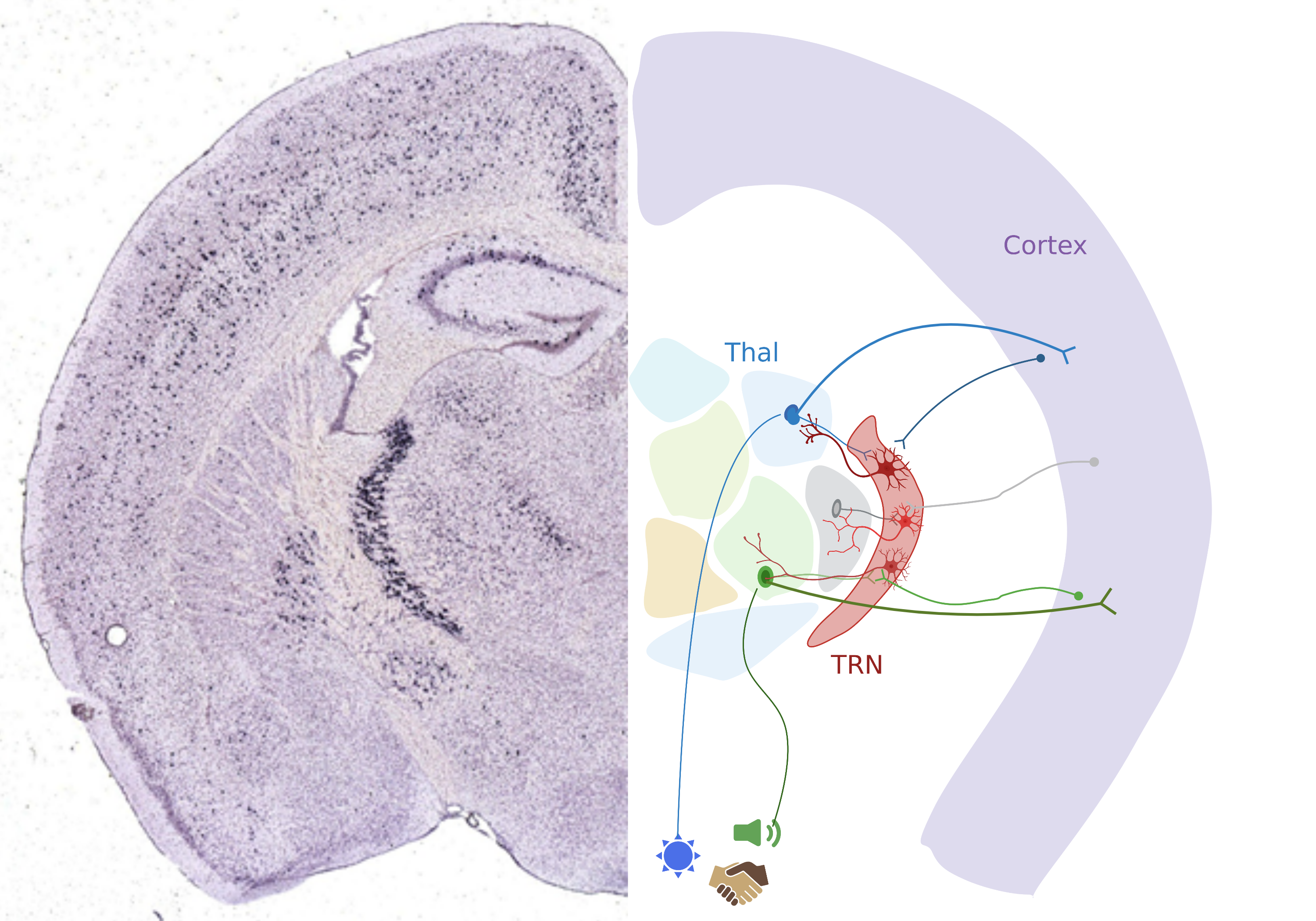
credit: Julie Haas
Electrical synapses
Electrical synapses are a major class of synapse formed by gap junctions between neurons. These gap junctions allow for electrical current to flow between two coupled neurons, allowing voltage differences to influence the activity of the cells.
A simple model of an electrical synapse can thus be a static resistance applied to the voltage difference between two neurons:
Computational models
My expertise with computational modelling is with utilizing the Hodgkin-Huxley (HH) based models. Neuron spiking is simulated from the biophysics of the sodium and potassium ion channels and their gating properties, mathematically described by Hodgkin and Huxley (1952).
The simplest example is shown here:
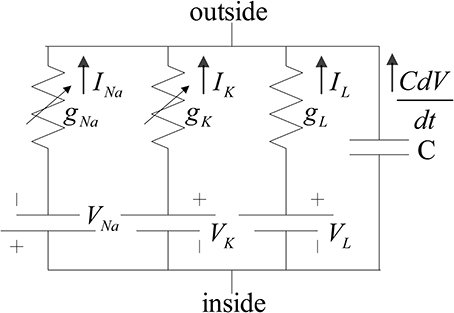
A basic solving interface for this system could be written as:
using OrdinaryDiffEq
prob = ODEProblem(dsim!, u0, (startTime, endTime), p)
# dsim: HH function to be solved
# u0: initial conditions
# p: parameters (channels, synapses etc.)
sol = solve(prob, BS3(), saveat=dt)where parameters (p) are:
struct HHmodel
gNa::Float64
gK::Float64
gL::Float64
ENa::Float64
EK::Float64
EL::Float64
C::Float64
Iapp::Float64
endand with the function dsim! describing the HH equations:
function dsim!(du, u, p, t)
v, n, m, h = u
I = (p.gK * (n^4.0) * (v-p.EK))
+ (p.gNa * (m^3.0) * h * (v-p.ENa))
+ (p.gL * (v-p.EL))
+ p.Iapp
du[1] = (-1.0/p.C) * I
du[2] = dn(v,n)
du[3] = dm(v,m)
du[4] = dh(v,h)
end
#dn,dm & dh dynamics ommited for clarity Solving the system with a positive square current illicits spiking such as:
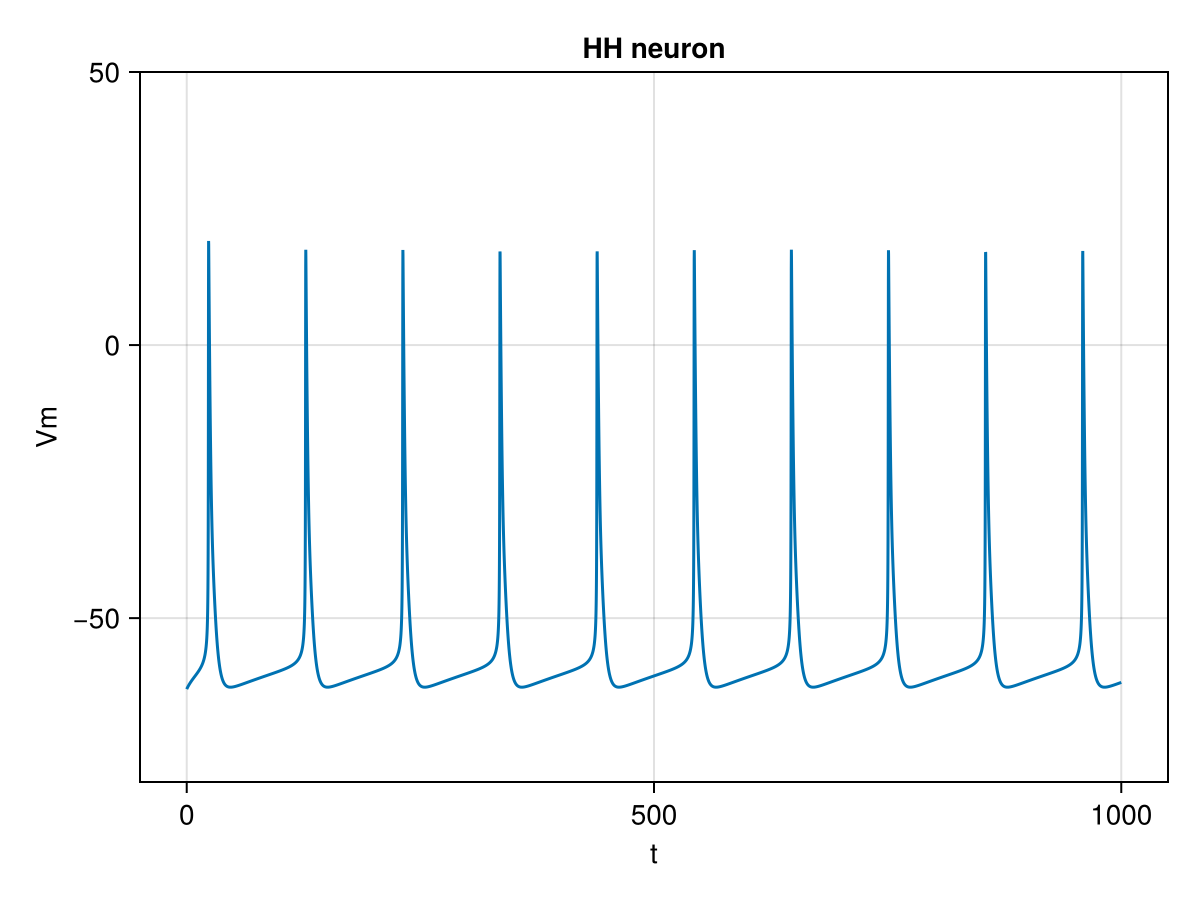
Interactive model
These interactive code notebooks have example HH and TRN neuron models where parameters can be explored.
